Today I learned about Berksons Paradox, a phenomenon in data where we see correlations that don’t really exist (or are even reversed) due to biases in how our data was sampled. I don’t know how I hadn’t come across this before but I’ve had some vague version of this idea in the back of my head for a while.

In data science we often get hyper-focused on this Kaggle-esque version of our work where we have a data set which we take for granted as being representative of the reality we want to model. But fundamentally there’ll always be some bias as to which events get translated into data and that puts some upper bound on the usefulness of our analysis.

I put together some simple code to illustrate this.

# Generate data
num_points = 100
x = np.random.uniform(-1, 1, num_points)
y = np.random.uniform(-1, 1, num_points)

# Assign points to four quadrants
quadrant1 = (x >= 0) & (y >= 0)
quadrant2 = (x < 0) & (y >= 0)
quadrant3 = (x < 0) & (y < 0)
quadrant4 = (x >= 0) & (y < 0)

data = {'X': x, 'Y': y}
df = pd.DataFrame(data)

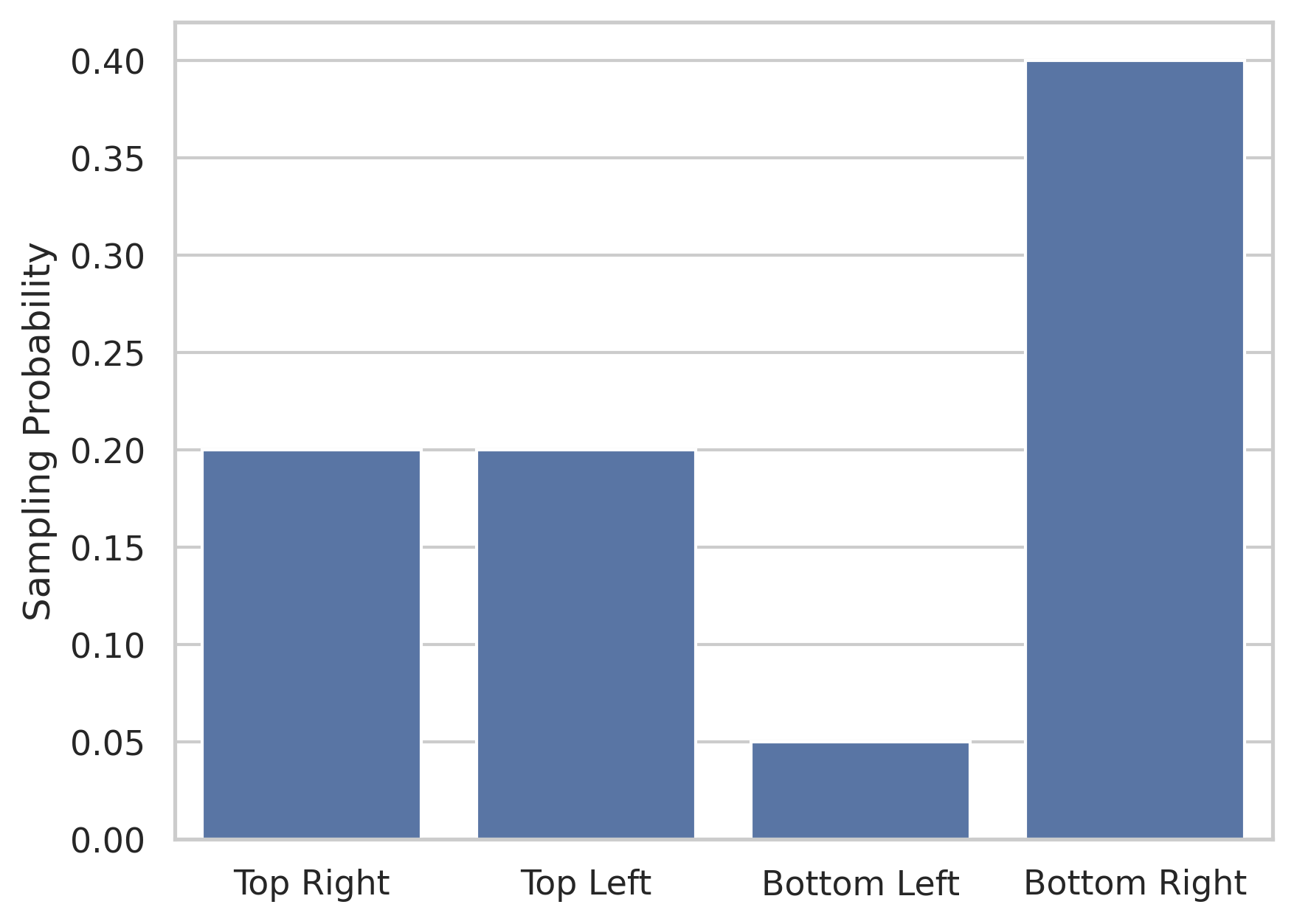
# Sample the data with different probability based on which quadrant
sampling_probabilities = [0.2, 0.2, 0.05, 0.4]
sampled_points = []

for quadrant, probability in zip([quadrant1, quadrant2, quadrant3, quadrant4], sampling_probabilities):
    sampled_points.extend(np.random.choice(np.arange(num_points)[quadrant], int(num_points/4 * probability), replace=False))

In this code I just set up a scatter plot with the randomly generated data.

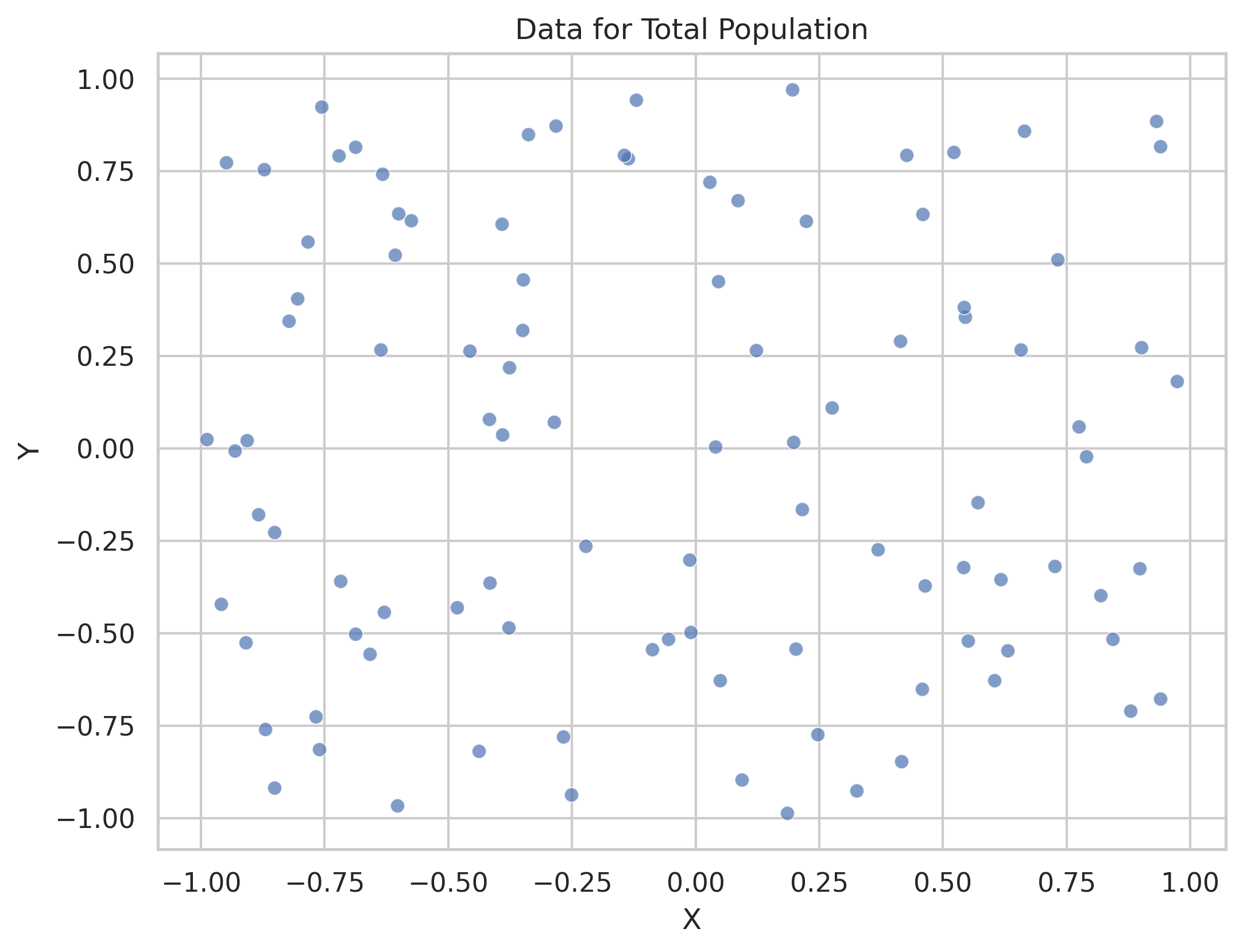
Random Data

Then I give each of the four quadrants of the data a different probability of being sampled.

Sampling Probabilities

When I do this sampling I then end up with a new scatter plot that makes it look like my data has a negative correlation.

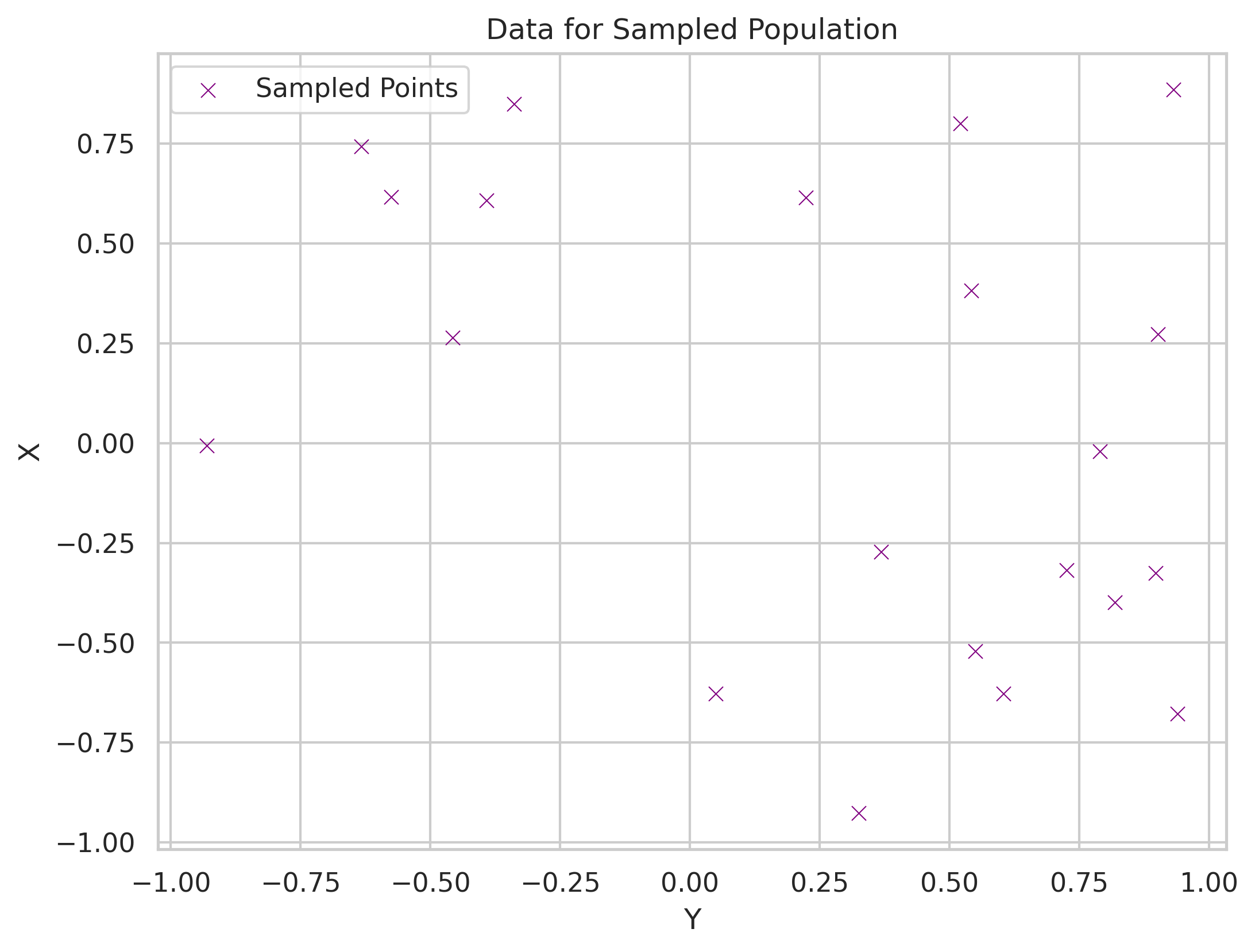
sampled Data

So, what do?

I don’t really have a good answer but this is something which has bothered me vaguelly for a while and will probably bother me more concretely now that I have a name for the phenomenon.

I think my core concern is that there is some information loss in going from the real-world to the data problems which data scientists focus on. Some amount of this can be mitigated by sitting and thinking carefully about the problem but I worry that when the fabricated correlation lines up with our expectations or intuition that we maybe don’t stare at the problem long enough to notice the issues.